Общие сведения о языке SFC

SFC (Sequential Function Chart) расшифровывается как «Последовательность функциональных диаграмм», и является одним из языков стандарта IEC 61131-3. SFC позволяет легко описывать последовательность протекания процессов в системе.

SFC осуществляет последовательное управление процессом, базируясь на системе условий, передающих управления с одной операции на другую. Язык SFC состоит из конечного числа базовых элементов, которые используются как блоки для построения целостного алгоритма протекания программы.

Основные понятия языка SFC

Язык SFC использует следующие структурные элементы для создания программы: шаг (и начальный шаг), переход, блок действий, прыжок и связи типа дивергенция и конвергенция.

После вызова программного модуля, описанного языком SFC, первым выполняется начальный шаг. Шаг, выполняемый в данный момент, называется активным. Действия, связанные с активным шагом, выполняются один раз в каждом управляющем цикле. В режиме выполнения активные шаги выделяются салатовым цветом. Следующий за активным шагом шаг станет активным, только если в переходе между этими шагами условие будет истинно.

В каждом управляющем цикле будут выполнены действия, содержащиеся в активных шагах. Далее проверяются условия перехода, и, возможно, уже другие шаги становятся активными, но выполняться они будут уже в следующем цикле.

Далее описывается каждый элемент SFC диаграммы.

Шаг

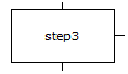
Наиболее важным элементом языка SFC является шаг, который описывает одну операцию. Шаг изображается в виде прямоугольника с собственным именем внутри (см. рис. 7.1).

Рис. 7.1 – Графическое представление «Шага» языка SFC

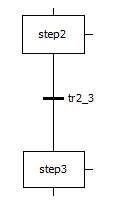
У каждого шага может быть 3 контакта. Сверху и снизу для соединения с переходом и справа для соединения с блоком действий. Шаг предваряется переходом, который определяет условие для активации данного шага в процессе выполнения программы и отображается в виде горизонтальной черты на ветви диаграммы процесса с указанием имени и условия. Два шага никогда не могут быть соединены непосредственно, они должны всегда отделяться переходом (см. рис. 7.2).

Рис. 7.2 – Шаги «step2» и «step3», соединённые переходом «tr2_3»

Любая SFC диаграмма должна содержать начальный шаг (шаг, выделенный двойной рамкой), с которого начинается выполнение диаграммы.

Переход

Между шагами находятся так называемые переходы. Условием перехода может быть логическая переменная или константа, логический адрес или логическое выражение, описанное на любом языке. Условие может включать серию инструкций, образующих логический результат, в виде ST выражения, например:

(i<= 100) AND b

либо на любом другом языке.

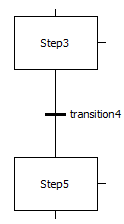
На рис. 7.3 приведён пример перехода между шагом «Step3» и «Step5» с именем «transition4».

Рис. 7.3 – Переход между шагами «Step3» и «Step5» с предопределённым условием «transition4»

В данном случае «transition4» это имя для предопределённого перехода, который может использоваться многократно на SFC диаграмме для определения переходов между несколькими шагами. Код для него может быть представлен, например, на языке ST:

:= (flag = True AND level > 10);

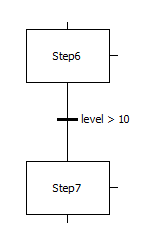
На рис. 7.4 представлен переход между шагами «Step6» и «Step7» в виде обычного условия:

level > 10

Рис. 7.4 – Переход между шагами «step6» и «step7» с предопределённым условием «transition4»

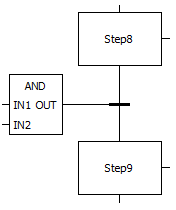
На рис. 7.5 представлен переход между шагами «Step8» и «Step9» в виде значения логического выражения «AND» на языке FBD:

Рис. 7.5 – Переход между шагами «step8» и «step9», заданный «логическим И» на языке FBD

Условие не должно содержать присваивания, вызов программ и экземпляров функциональных блоков.

Блок действий

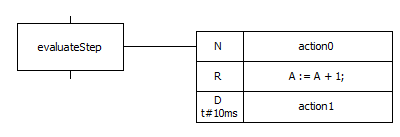
Каждый шаг имеет нулевое или большее количеством действий, объединённых, как правило, на диаграмме, в блок действий. На рис. 7.6 показан примера шага «evaluateStep» и связанный с ним блок действий.

Рис. 7.6 – Шаг «evaluateStep» и связанный с ним блок действий, содержащий 3 действия

Блок действий определяет операции, которые должны выполняться при активации (выполнении) шага. Шаги без связанного блока действий идентифицируются как ждущий шаг. Блок действий может состоять из предопределённых действий. Каждому предопределённому действию присваивается имя (на рис. 7.6 это «action0» и «action1»). Одно действие может использоваться сразу в нескольких шагах. Действие может выполняться непрерывно, пока активен шаг, либо единожды. Это определяется специальными квалификаторами, описание которых приведено в таблице 6. Квалификаторы также могут ограничивать время выполнения каждого действия в шаге.

«Прыжок» – переход на произвольный шаг

Шаг может быть также заменён «прыжком». Последовательности шагов всегда ассоциируются с прыжком к другому шагу той же самой последовательности шагов. Это означает, что они выполняются циклически. Переход на произвольный шаг – это соединение на шаг, имя которого указано под знаком «прыжка». Такие переходы нужны для того, чтобы избежать пересекающихся и идущих вверх соединений. На рис. 7.7 показана SFC диаграмма, содержащая два «прыжка».

Рис. 7.7 – SFC диаграмма, содержащая «прыжки»

Первый делает переход к шагу «init» в случае выполнения условия «transition4», второй делает переход к шагу «step1», в случае выполнения условия «transition2».

Дивергенция и конвергенция

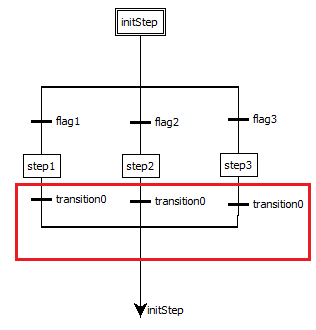
Дивергенция – это множественное соединение в направлении от одного шага к нескольким переходам. Активируется только одна из ветвей. Условия, связанные с различными переходами в начале дивергенции, не являются взаимоисключающими по умолчанию. Взаимоисключение должно быть явно задано в условиях переходов, чтобы гарантировать, что во время выполнения программы активируется одна конкретная ветвь. Пример дивергенции на SFC диаграмме приведён на рис. 7.8 и выделен красным цветом:

Рис. 7.8 – Дивергенция на SFC диаграмме

Конвергенция – это множественное соединение, направленное от нескольких переходов к одному и тому же шагу. Она обычно используется для группировки ветвей SFC – программы, которые берут начало из одинарной дивергенции. Пример конвергенции на SFC диаграмме приведён на рис. 7.9 и выделен красным цветом:

Рис. 7.9 – Конвергенция на SFC диаграмме

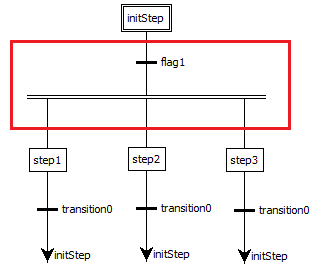
Параллельная дивергенция – это множественное соединение, направленное от одного перехода к нескольким шагам. Она соответствует параллельному выполнению операций процесса. Пример параллельной дивергенции на SFC диаграмме приведён на рис. 7.10 и выделен красным цветом:

Рис. 7.10 – Параллельная дивергенция на SFC диаграмме

Параллельная конвергенция – это соединение нескольких шагов к одному и тому же переходу. Обычно она используется для группирования ветвей, взявших начало дивергенции. Пример параллельной конвергенции на SFC диаграмме приведён на рис. 7.11 и выделен красным цветом:

Рис. 7.11 – Параллельная конвергенция на SFC диаграмме

Пример программы на языке SFC

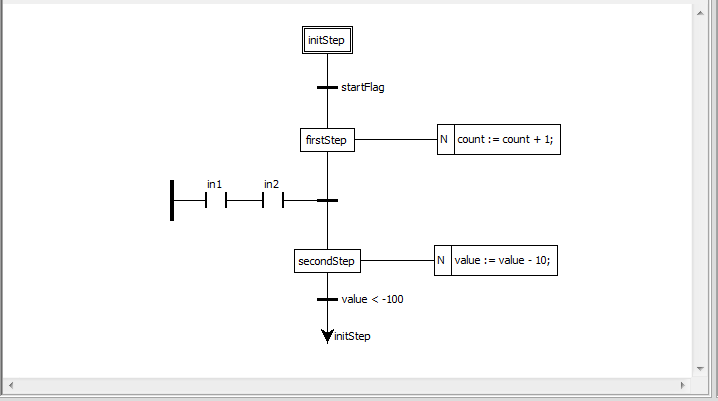
На рис. 7.12 приведен пример SFC диаграммы состоящей из начального шага «initStep», шагов «firstStep» и «secondStep» и 3 перехода.

Переход «startFlag» представляет обычную переменную типа BOOL и полностью зависит от её значения. Переход между «firstStep» и «secondStep» зависит от LD диаграммы с двумя катушками, ассоциированными с переменными типа BOOL: «in1» и «in2». Переход активируется только в том случае, если «in1» и «in2» будут TRUE. Переход между «secondStep» и прыжком на initStep активирован, когда значение переменной «value» меньше -100.

Во время действия «firstStep» выполняется увеличение переменной count на 1. Во время действия «secondStep» из переменной «value» вычитается 10.

Рис. 7.12 – SFC диаграмма